The Signal Protocol used by 1+ billion people is getting a post-quantum makeover

The Signal Foundation, maker of the Signal Protocol that encrypts messages sent by more than a billion people, has rolled out an update designed to prepare for a very real prospect that’s never far from the thoughts of just about every security engineer on the planet: the catastrophic fall of cryptographic protocols that secure some of the most sensitive secrets today.

The Signal Protocol is a key ingredient in the Signal, Google RCS, and WhatsApp messengers, which collectively have more than 1 billion users. It’s the engine that provides end-to-end encryption, meaning messages encrypted with the apps can be decrypted only by the recipients and no one else, including the platforms enabling the service. Until now, the Signal Protocol encrypted messages and voice calls with X3DH, a specification based on a form of cryptography known as Elliptic Curve Diffie-Hellman.

A brief detour: WTF is ECDH?

Often abbreviated as ECDH, Elliptic Curve Diffie-Hellman is a protocol unto its own. It combines two main building blocks. The first involves the use of elliptic curves to form asymmetric key pairs, each of which is unique to each user. One key in the pair is public and available to anyone to use for encrypting messages sent to the person who owns it. The corresponding private key is closely guarded by the user. It allows the user to decrypt the messages. Cryptography relying on a public-private key pair is often known as asymmetric encryption.

The security of asymmetric encryption is based on mathematical one-way functions. Also known as trapdoor functions, these problems are easy to compute in one direction and substantially harder to compute in reverse. In elliptic curve cryptography, this one-way function is based on the Discrete Logarithm problem in mathematics.The key parameters are based on specific points in an elliptic curve over the field of integers modulo some prime P.

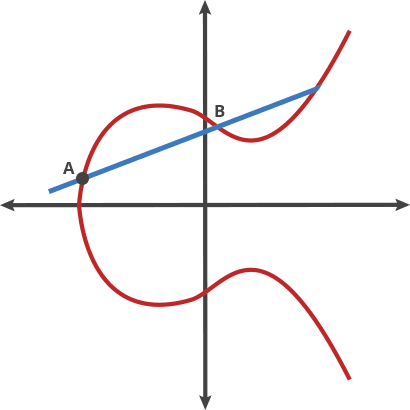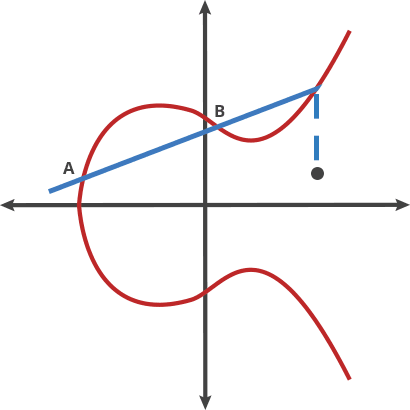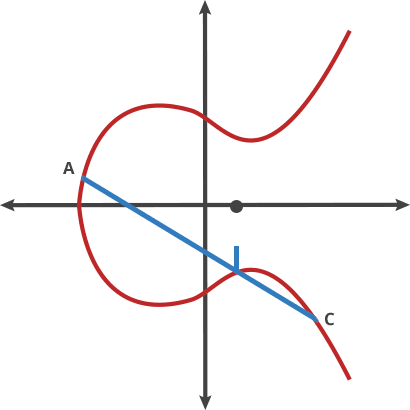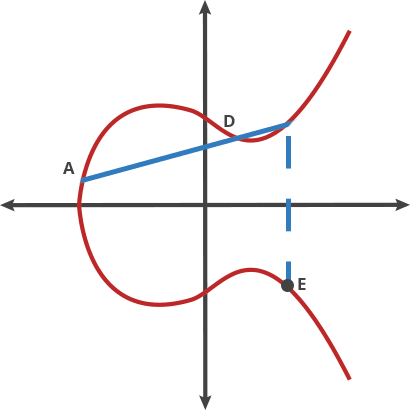
When someone knows the starting point (A) in the above image showing an elliptic curve and the number of hops required to get to the endpoint (E), it’s easy to know where (E) is. But when all someone knows is the starting and end points, it’s next to impossible to deduce how many hops are required.

As explained in an Ars article from 2013:

Let's imagine this curve as the setting for a bizarre game of billiards. Take any two points on the curve and draw a line through them; the line will intersect the curve at exactly one more place. In this game of billiards, you take a ball at point A and shoot it toward point B. When it hits the curve, the ball bounces either straight up (if it's below the x-axis) or straight down (if it's above the x-axis) to the other side of the curve.

We can call this billiards move on two points "dot." Any two points on a curve can be dotted together to get a new point.

A dot B = C

We can also string moves together to "dot" a point with itself over and over.

A dot A = B

A dot B = C

A dot C = D

...

It turns out that if you have two points, an initial point "dotted" with itself n times to arrive at a final point, finding out n when you only know the final point and the first point is hard. To continue our bizarro billiards metaphor, imagine that one person plays our game alone in a room for a random period of time. It is easy for him to hit the ball over and over following the rules described above. If someone walks into the room later and sees where the ball has ended up, even if they know all the rules of the game and where the ball started, they cannot determine the number of times the ball was struck to get there without running through the whole game again until the ball gets to the same point. Easy to do, hard to undo. This is the basis for a very good trapdoor function.

Safe... but for how much longer?

The one-way function for RSA works in a similar manner but relies on the multiplication and factorization of large prime numbers. It is computationally easy to multiply two large primes together to compute their product, but it's much more computationally intensive to find the original primes from their product.

Asymmetric cryptography is ideal for confidentiality on the Internet because it solves the challenge of securely exchanging keys through an untrusted medium among two or more people who have never met. The robustness of these forms of encryption, however, breaks down in quantum computing. Under a concept known as superposition, the 0 and 1 binary bits found in classical computing are replaced with qubits, where 0s and 1s can in essence exist in multiple states at once.

A factorization method known as Shor’s algorithm is widely believed to make it possible for a quantum computer with a sufficient number of qubits to break asymmetric encryption based on the difficulty of solving one-way functions. The current estimate is that to break RSA encryption with either 1,024 or 2,048 bits, it would take a quantum computer with about 20 million qubits running in superposition for about eight hours.

Currently, the largest quantum computer known to be in existence today runs with just 433 qubits. Estimates vary widely as to how long it will be until there’s a large and robust enough quantum computer to break ECC and other vulnerable algorithms. Some expert forecasts predict as few as five years, while others say it could be 30 or more years out.

Enter PQC

There is little disagreement, however, that there will come a day when many of the most widely used forms of encryption will die at the hands of quantum computing. To head off that doomsday eventuality, engineers and mathematicians have been developing a new class of PQC, short for post-quantum cryptography.

The PQC added to the Signal Protocol on Monday is called PQXDH. It uses the same X3DH specification the Signal Protocol has always employed. On top, it adds an additional layer of encryption using Crystals-Kyber, one of four PQC algorithms the National Institute of Standards and Technology selected last year as a potential replacement to ECC and other quantum-vulnerable forms of encryption.

In a post published Tuesday, Signal Foundation CTO Ehren Kret wrote:

We believe that the key encapsulation mechanism we have selected, CRYSTALS-Kyber, is built on solid foundations, but to be safe we do not want to simply replace our existing elliptic curve cryptography foundations with a post-quantum public key cryptosystem. Instead, we are augmenting our existing cryptosystems such that an attacker must break both systems in order to compute the keys protecting people’s communications.

The essence of our protocol upgrade from X3DH to PQXDH is to compute a shared secret, data known only to the parties involved in a private communication session, using both the elliptic curve key agreement protocol X25519 and the post-quantum key encapsulation mechanism CRYSTALS-Kyber. We then combine these two shared secrets together so that any attacker must break both X25519 and CRYSTALS-Kyber to compute the same shared secret.

There’s good reason for using both ECC and CRYSTALS-Kyber. Less than two months after NIST last year selected the four PQC algorithm candidate replacements, one of them was taken out of the running after researchers devised a technique that used complex mathematics and a single traditional PC to recover the encryption keys underlying the algorithm. The spectacular downfall of SIKE—as the PQC algorithm is known—underscores the risks inherent in the transition away from traditional forms of cryptography.

A PQC algorithm Google has proposed for the FIDO2 industry standard for logging in to websites takes a similar approach. It combines the Elliptic Curve Signature Algorithm with CRYSTALS-Dilithium, one of the other three PQC algorithms still under consideration by NIST.

For now, the Signal app will use both the X3DH and the PQXDH. When all parties in a discussion have new versions of Signal installed, PQXDH will be used. When one or more of the parties are using older versions, conversations will be encrypted with X3DH. Eventually, Kret said he expects the Signal Protocol will use only the newer algorithm.

“We will need to make further upgrades to address the threat of an attacker with a contemporaneous quantum computer,” the CTO wrote. “Further research in the area of post-quantum cryptography will be needed to fill in the remaining gaps.”